Vous avez peut-être déjà rencontré le terme « sigma » dans le contexte d’une découverte réalisée en physique des particules. Mais que veut-il dire exactement ? Pourquoi est-il si important de mentionner les sigmas lors de l’annonce de la découverte d’une nouvelle particule ? Et pourquoi cinq sigmas spécifiquement ?

Pourquoi la physique des particules s’appuie-t-elle sur les statistiques ?

Les particules produites lors de collisions au Grand collisionneur de hadrons (LHC) sont minuscules et ont une durée de vie extrêmement courte. Elles se désintègrent presque immédiatement en d’autres particules, et il est donc impossible de les « voir » directement. À la place, ce qu’observent les physiciens, ce sont les propriétés des particules finales, notamment leur charge, leur masse, leur spin et leur vitesse. Comme des détectives, ils étudient les produits finaux à la recherche d’indices sur les éventuelles transformations subies par les particules au cours de leur désintégration. Les probabilités concernant ces « canaux de désintégration » sont prédites par la théorie.

Au LHC, des millions de collisions de particules sont filtrées à chaque seconde grâce à des systèmes de déclenchement conçus pour identifier la désintégration des particules rares. Ensuite, les équipes analysent les données filtrées pour trouver des anomalies qui pourraient indiquer la présence d’une nouvelle physique.

Comme dans toute expérience, il y a toujours une possibilité d’erreur. Ainsi, le bruit de fond peut provoquer des fluctuations naturelles dans les données, ce qui aboutira à des erreurs statistiques. Le risque d’erreur peut venir du fait que la quantité de données est insuffisante ; ou bien, des équipements défectueux ou de petites erreurs de calcul peuvent être à l’origine d’erreurs systématiques. Les scientifiques cherchent des moyens de réduire l’incidence de ces erreurs pour pouvoir revendiquer des résultats avec autant d’exactitude que possible.

Qu’est-ce que la signification statistique ?

Prenons un dé normal à six faces : si vous le lancez, vous avez une chance sur six d’obtenir un chiffre en particulier. Par contre, si vous lancez deux dés, la probabilité d’obtenir un total donné varie : il n’y a qu’une seule façon d’obtenir un deux, contre six façons différentes d’obtenir un sept. Supposons que vous lancez ces deux dés à de très nombreuses reprises et que vous présentez les résultats sous forme de graphique, vous obtiendrez une courbe en cloche également appelée distribution normale.

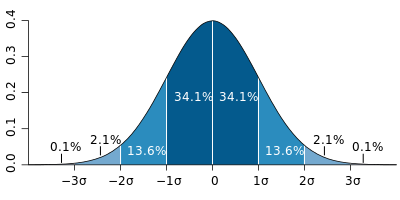
La distribution normale possède des propriétés intéressantes : elle est symétrique, son pic correspond à la moyenne, et la dispersion des données est mesurée à l’aide de l’écart-type. Pour des données présentant une distribution normale, la probabilité de voir un point de données se situer dans la limite d’un écart-type par rapport à la moyenne est de 68 %. Cette probabilité monte à 95 % pour deux écarts-types et est encore plus élevée pour trois écarts-types.

L’écart-type est représenté par la lettre grecque σ (sigma). La signification statistique, mesurée par le nombre d’écarts-types par rapport à la moyenne, désigne la distance entre un point de données spécifique et sa valeur attendue.

Quel rapport avec la physique ?

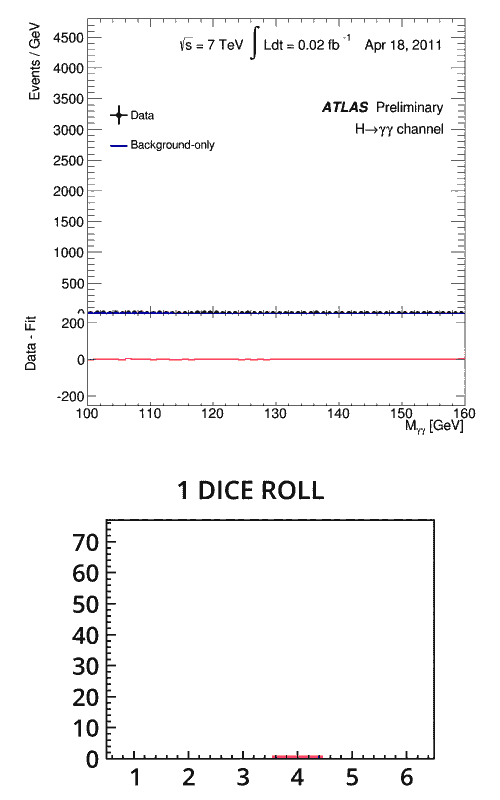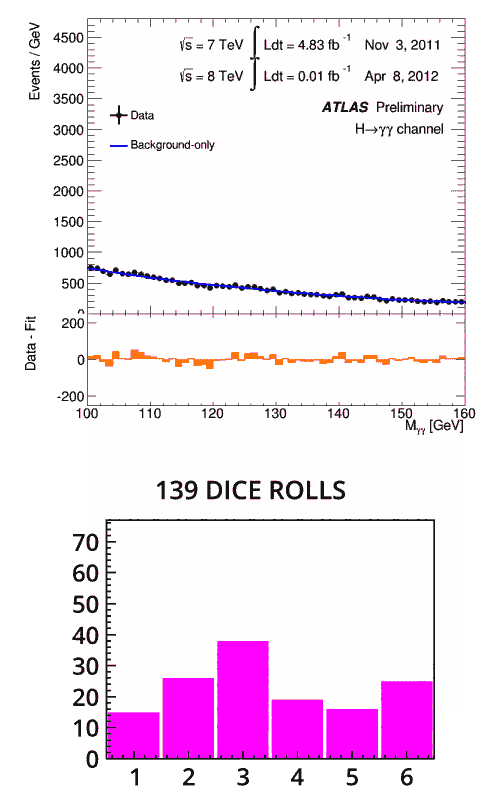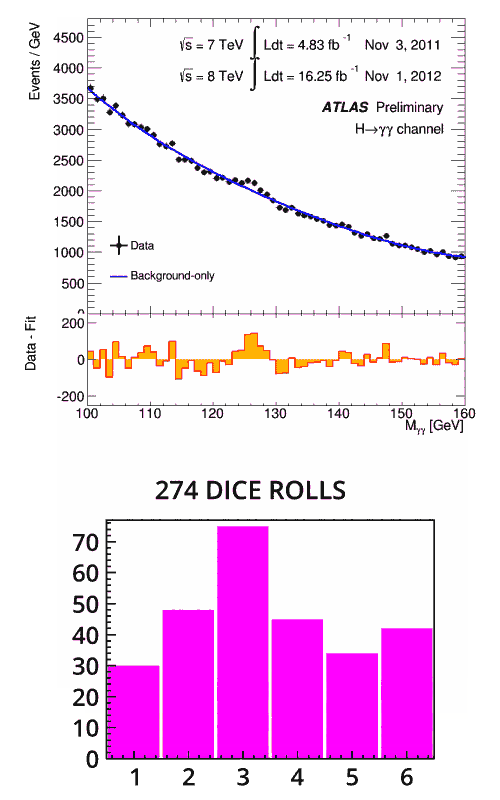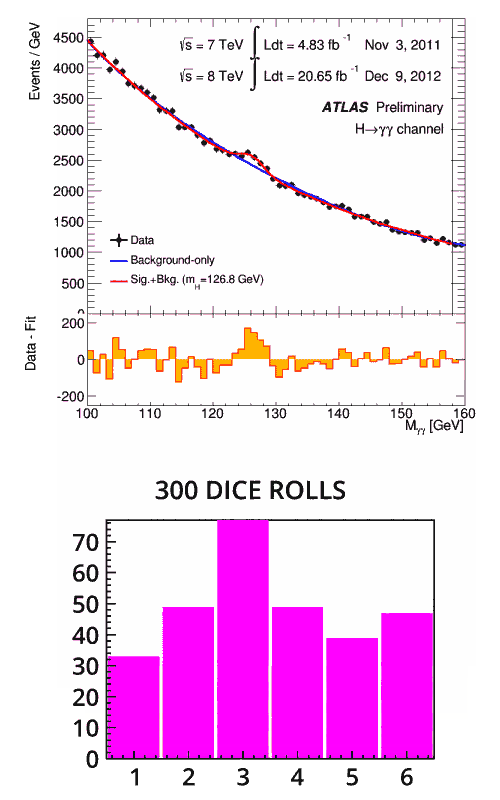
Lorsque les scientifiques examinent les données enregistrées au LHC, il est normal qu’ils observent de petites bosses et des fluctuations statistiques, mais les résultats sont généralement proches de la valeur attendue. Une anomalie plus importante indique la présence d’un nouveau résultat. À quel moment cette anomalie peut-elle être considérée comme un nouveau phénomène ? Pour le découvrir, les scientifiques s’appuient sur les statistiques.

Revenons à notre analogie avec le dé. Cette fois, vous lancez un dé en ne sachant pas s’il est truqué, et vous obtenez un trois au premier lancer. Ce résultat n’est pas particulièrement significatif, puisque vous aviez une chance sur six d’obtenir un trois : vous avez besoin de davantage de données pour déterminer si le dé est bel et bien truqué. Vous lancez le dé deux fois, trois fois, voire plus : à chaque fois, il donne un trois. À quel moment pouvez-vous confirmer que le dé est truqué ?

Il n’existe aucune règle en la matière mais si vous obtenez le même résultat, disons, huit fois de suite, vous n’aurez plus guère de doute. La probabilité qu’un tel résultat se produise par hasard n’est que de (1/6)⁸ = 0,00006 %.

Les physiciens procèdent de la même façon pour déterminer si une anomalie constitue vraiment un résultat. Plus les données sont nombreuses, plus la probabilité que se produise une fluctuation statistique à un moment donné diminue. Dans le cas du boson de Higgs, les physiciens avaient besoin d’une quantité suffisante de données pour que la signification statistique dépasse le seuil des cinq sigmas. Ce n’est qu’à ce moment-là qu’ils ont pu annoncer la découverte d’une « particule aux caractéristiques compatibles avec celles du boson de Higgs ».

Que veut dire « signification statistique de cinq sigmas » ?

Si l’on obtient un résultat avec une signification statistique de cinq sigmas, cela signifie qu’il est quasi-certain que la bosse observée sur la courbe des données est due à un nouveau phénomène et non à une fluctuation statistique. Pour calculer la signification statistique, les scientifiques mesurent le signal en le comparant aux fluctuations attendues du bruit de fond sur toute l’étendue des données. Pour certains résultats, dont les anomalies pourraient se situer au-dessus comme au-dessous de la valeur attendue, une signification de cinq sigmas représente la probabilité de 0,00006 % que les données soient des fluctuations. Pour d’autres, comme la découverte du boson de Higgs, une signification de cinq sigmas indique une probabilité de 0,00003 % d’une fluctuation statistique, car les scientifiques cherchent des données ayant une signification de plus de cinq sigmas sur une moitié de la courbe de distribution normale.

Pourquoi veut-on spécifiquement cinq sigmas en physique des particules ?

Dans la plupart des domaines scientifiques qui utilisent l’analyse statistique, ce seuil de cinq sigmas semble excessif. En règle générale, pour une étude sur la population, par exemple un sondage sur les intentions de vote, un résultat possédant une signification statistique de trois sigmas suffirait. Néanmoins, quand il s’agit de décrire le matériau qui compose l’Univers, les scientifiques s’efforcent d’être aussi précis que possible. Les connaissances scientifiques relatives à la nature fondamentale de la matière ont un impact important et une erreur pourrait avoir des répercussions considérables.

Par le passé, il est arrivé que des résultats, semblant révéler de nouvelles découvertes, soient annoncés sur la base de données dont la signification statistique n’était que de trois ou quatre sigmas, et que ces résultats soient ultérieurement démentis une fois analysé un volume de données plus important.

En cas d’erreur systématique, due à une erreur de calcul par exemple, une signification initiale élevée de cinq sigmas peut indiquer que les résultats ne sont pas totalement dénués de validité. Toutefois, cela veut dire que le résultat n’est pas certain et qu’il ne peut servir à revendiquer une nouvelle découverte.

La valeur de cinq sigmas est considérée comme la référence en physique des particules, car elle garantit une très faible probabilité que l’observation soit fausse.

Mais cinq sigmas ne suffisent pas toujours...

En règle générale, cinq sigmas représentent la valeur de signification statistique acceptée pour la découverte de nouvelles particules s’inscrivant dans le Modèle standard, c’est-à-dire de particules prédites par la théorie qui représente notre compréhension actuelle de la nature. Une signification de cinq sigmas est également admise pour la recherche de propriétés spécifiques du comportement des particules, car la probabilité de trouver des fluctuations dans l’échantillon est moindre.

Pour déterminer si une signification statistique de cinq sigmas est suffisante, il convient de comparer, en s’appuyant sur la théorie, la probabilité de la réalisation d’une nouvelle hypothèse avec celle d’une fluctuation statistique.

En ce qui concerne la physique au-delà du Modèle standard ou les données qui contredisent la physique généralement admise, la signification statistique doit être beaucoup plus élevée, assez pour « réfuter » la physique précédente. Dans son article intitulé « Discovering the Significance of 5 Sigmas », le physicien Louis Lyons suggère que les résultats correspondant à des phénomènes moins probables devraient être contraints à une signification statistique plus élevée : sept sigmas pour la détection d’ondes gravitationnelles ou la découverte de pentaquarks, par exemple.

Louis Lyons estime toutefois dans son article qu’une signification statistique de cinq sigmas est suffisante pour la découverte du boson de Higgs. En effet, la théorie du boson de Higgs a été prédite, testée mathématiquement et généralement admise par la communauté de la physique des particules bien avant que le LHC puisse créer les conditions permettant de l’observer. Mais une fois le signal détecté, une signification statistique élevée était tout de même nécessaire pour affirmer qu’il s’agissait d’une découverte.

___________________________________________________________________________

Une signification statistique de cinq sigmas est une contrainte rigoureuse, mais cette valeur est en fait un minimum ; une valeur plus élevée confère encore plus de fiabilité aux données. Néanmoins, pour obtenir des résultats avec une signification statistique de six, sept, voire huit sigmas, il faut beaucoup plus de données, et y consacrer plus de temps et d’énergie. C’est pourquoi une probabilité de 0,00006 % au plus qu’un nouveau phénomène ne soit pas un aléa statistique est suffisante.

Pour en savoir plus :

• Article : « Discovering the Significance of 5 Sigmas » (en anglais)
• Vidéo : The Higgs Discovery Explained (en anglais)
• Article en ligne : One- and Two-Tailed Tests (en anglais)